Implicit Wiener Series for higher-order image analysis
HTWG Konstanz, Brauneggerstr. 55, D-78462
Max-Planck-Institute for Biological Cybernetics, Spemannstr. 38, D-72076
Volterra and Wiener series
In system
identification, one tries to infer the functional relationship between system
input and output from observations of the in- and outgoing signals. If the
system is linear, it can be characterized uniquely by measuring its impulse
response, for instance by reverse correlation. For nonlinear systems, however,
there exists a whole variety of system representations. One of them, the Wiener
expansion, has found a somewhat wider use in neuroscience since its
estimation constitutes a natural extension of linear system identification. The
coefficients of the Wiener expansion can be estimated by a cross-correlation
procedure that is conveniently applicable to experimental data.
Unfortunately, the estimation of the Wiener expansion by cross-correlation
suffers from severe problems:
- In practice, the cross-correlations have to be
estimated at a finite resolution. The number of expansion coefficients
increases with mn for an m-dimensional
input signal and an nth-order Wiener kernel such that the resulting
numbers are huge for higher-order Wiener kernels. For instance, a
5th-order Wiener kernel operating on 16 x 16 sized image patches contains
roughly 1012 coefficients, 1010 of which would have
to be measured individually by cross-correlation. As a consequence, this
procedure is not feasible for higher-dimensional input signals.
- The estimation of cross-correlations requires
large sample sizes. Typically, one needs several tens of thousands of
input-output pairs before a sufficient convergence is reached.
- The estimation via cross-correlation works only
if the input is Gaussian noise with zero mean, not for general types of
input.
- The crosscorrelation
method assumes noise-free signals. For real, noise-contaminated data, the
estimated Wiener series models both signal and noise of the training data
which typically results in reduced prediction performance on independent
test sets.
A brief tutorial on Volterra and Wiener series can be found in
[1] Franz, M.O. and B. Schölkopf:
Implicit Wiener Series. MPI Technical Report (114), Max Planck Institute for Biological
Cybernetics,
Implicit
estimation via polynomial kernels
We propose a new estimation method based on regression in a
reproducing kernel Hilbert space (RKHS) to overcome these problems. Instead of
estimating each expansion coefficient individually by cross-correlation, we
treat the Wiener series as a linear operator in the RKHS formed by the
monomials of the input. The Wiener expansion can be found by computing the
linear operator in the RKHS that minimizes the mean square error. Since the
basis functions of the Wiener expansion (i.e. the monomials of the components
of the input vector) constitute a RKHS, one can represent the Wiener
series implicitly as a linear combination of scalar products in the RKHS. It
can be shown that the orthogonality properties of the
Wiener operators are preserved by the estimation procedure.
In contrast to the classical cross-correlation method, the implicit
representation of the Wiener series allows for the identification of systems
with high-dimensional input up to high orders of nonlinearity. As an example,
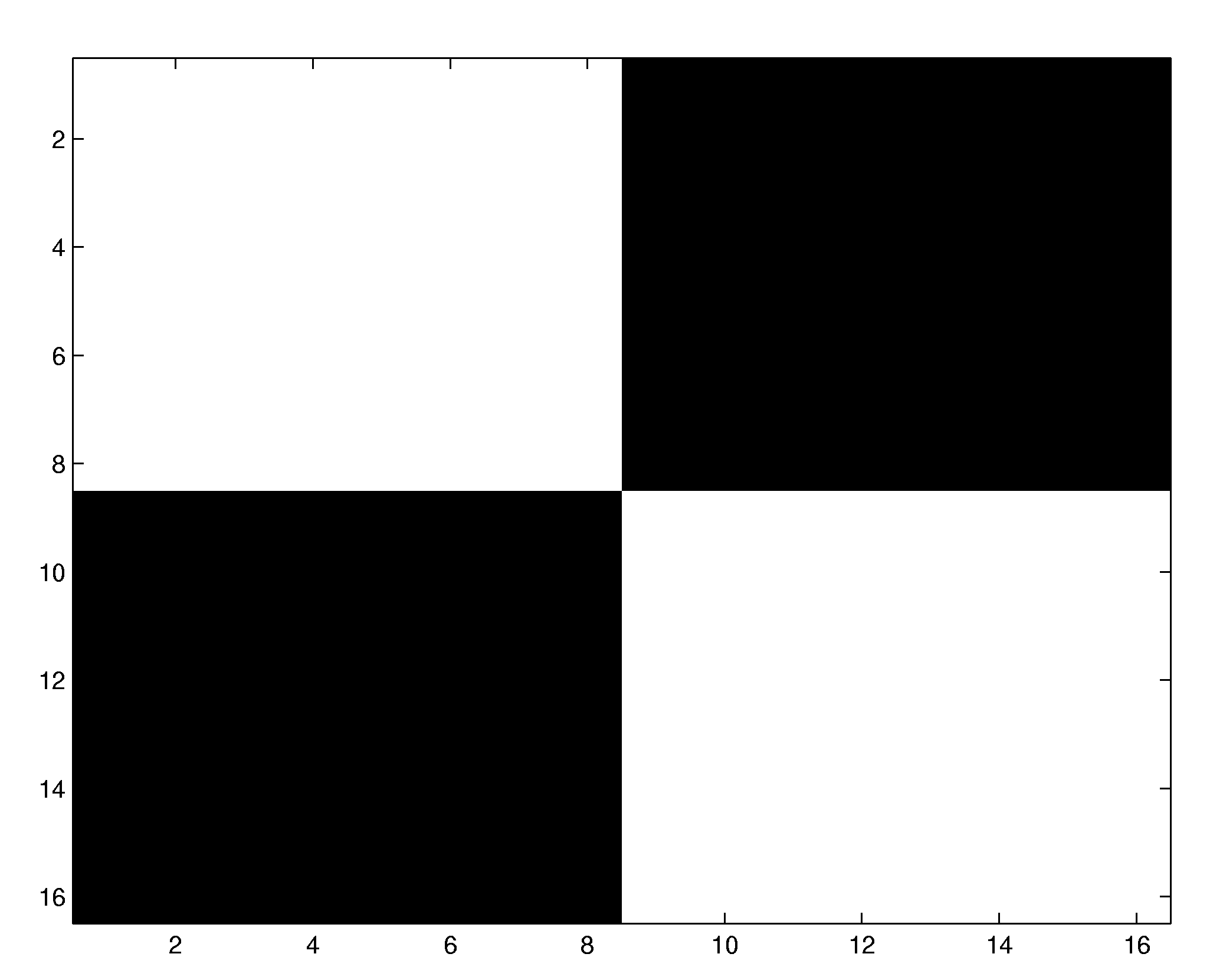
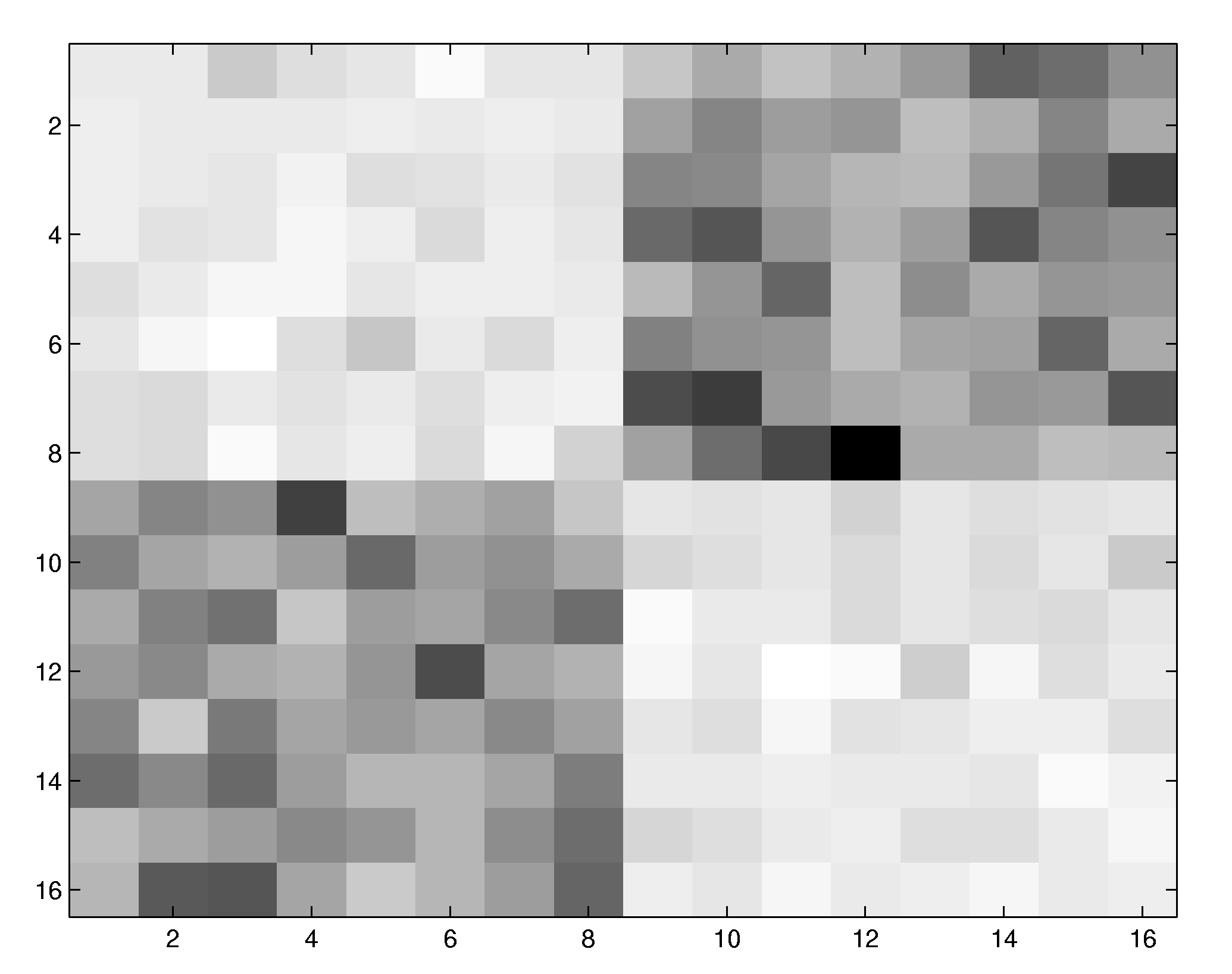
we have computed a nonlinear receptive field of a 5th-order system acting on 16
x 16 image patches. The system first convolves the input with the filter mask
shown below to the right and feeds the result in a fifth-order
nonlinearity. In the classical cross-correlation procedure, the system
identification would require the computation of roughly 9.5 billion independent
terms for the fifth-order Wiener kernel, and several tens of thousands of data
points. Using the new estimation method, the structure of the nonlinear
receptive field becomes already recognizable after 2500 data points.
|
Original convolution mask |
Reconstructed nonlinear receptive
field |
The
implicit estimation method is described in
[2] Franz, M.
O. and B. Schölkopf: A unifying view of Wiener and Volterra theory and polynomial kernel regression. Neural
Computation 18(12), 3097-3118 [PDF].
[3] Franz,
M.O. and B. Schölkopf: Implicit estimation of Wiener
series. Machine Learning for Signal Processing XIV, Proc.
2004 IEEE Signal Processing Society Workshop, 735-744. (Eds.) Barros, A., J.
Principe, J. Larsen, T. Adali and S. Douglas, IEEE,
A package
of Matlab routines for polynomial Gaussian process
regression and estimation of Volterra kernels can be
found here.
Higher-order statistics of natural images
The
implicit estimation of Wiener operators via polynomial kernels opens up new
possibilities for the estimation of higher-order image statistics. Compared to
the classical methods such as higher-order spectra, moments or cumulants, our approach avoids the combinatorial explosion
caused by the exponential increase of the number of terms to be estimated and
interpreted. When put into a predictive framework, multiplicative pixel
interactions of different orders are easily visualized and conform to the intuitive
notions about image structures such as edges, lines, crossings or corners.
Arbitrarily oriented lines and edges, for instance, cannot be described by the
usual pairwise statistics such as the power spectrum
or the autocorrelation function: From knowing the intensity of one point on a
line alone, we cannot predict its neighbouring
intensities. This would require knowledge of a second point on the line, i.e.,
we have to consider some third-order statistics which describe the interactions
between triplets of points. Analogously, the prediction of a corner neighbourhood needs at least fourth-order statistics, and
so on.
This can be seen in the following experiment, where we decomposed various toy
images into their components of different order.

The behaviour of the models conforms to our
intuition: the linear model cannot capture the line structure of the image thus
leading to a large reconstruction error which drops to nearly zero when a
second-order model is used. Note that the third-order component is only
significant at crossings, corners and line endings.
Pixel interactions up to the order of five play an important role in natural
images. Here is an example decomposition:

Reference:
[4] Franz, M.O. and B. Schölkopf: Implicit Wiener series for
higher-order image analysis. Advances in Neural Information
Processing Systems 17, 465-472. (Eds.) Saul,
L.K., Y. Weiss and L. Bottou, MIT Press,
Robust estimation with polynomial kernels
The use of
a non-orthonormal function dictionary such as
polynomials in ridge regression leads to a non-isotropic prior in function
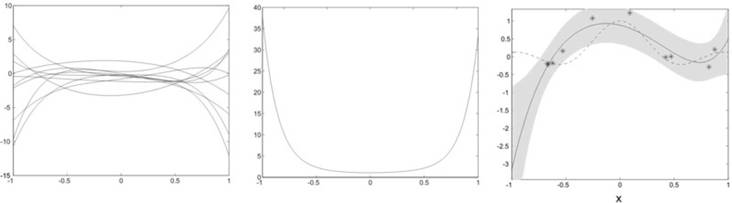
space. This can be seen in a simple toy example where the function to be
regressed is a sinc function with uniformly
distributed input and additive Gaussian noise. Our function dictionary consists
of the first six canonical which are neither orthogonal nor normalized with
respect to the uniform input. The effects on the type of functions that can be
generated by this choice of dictionary can be seen in a simple experiment: we
assume random weights distributed according to an isotropic Gaussian. In our
first experiment, we draw samples from this distribution and compute the mean
square of the for 1000 functions generated by the
dictionary. It is immediately evident that, given a uniform input, our prior
narrowly constrains the possible solutions around the origin while admitting a
broad variety near the interval boundaries. If we do ridge regression with this
dictionary (here we used a Gaussian Process regression scheme), the solutions
tend to have a similar behaviour as long as they are
not enough constrained by the data points (see the diverging solution at the
left interval boundary). This can lead to bad predictions in sparsely populated
areas.
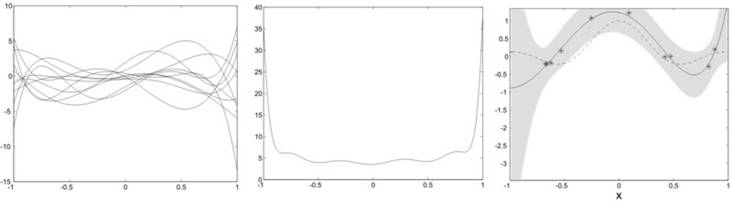
We
currently investigate alternative regularization techniques that result in an
implicit whitening of the basis functions by penalizing directions in function
space with a large prior variance. The regularization term can be computed from
unlabelled input data that characterizes the input distribution. Here, we
observe a different behaviour: the functions sampled
from the prior show a richer structure with a relatively flat mean square value
over the input interval. As a consequence, the ridge regression solution
usually does not diverge as easily in sparsely populated regions near the
interval boundaries.
Reference:
[5] Franz, M.O., Y. Kwon, C. E.
Rasmussen and B. Schölkopf:
Semi-supervised kernel regression using whitened function classes. Pattern Recognition,
Proceedings of the 26th DAGM Symposium LNCS 3175, 18-26. (Eds.)
Rasmussen, C. E., H. H. Bülthoff, M. A. Giese and B. Schölkopf,
Springer, Berlin, Germany (2004)
[PDF]