Zur
Anwendung der Finite-Element-Methode in der Praxis
-
Fehlerquellen bei der Modellbildung und Ergebnisinterpretation -
Prof.
Dr.-Ing. Horst
Werkle, 78476 Allensbach
Dipl.-Ing.
Peter Bock, Peter & Lochner,
Beratende Ingenieure VBI, 70184 Stuttgart
Vortrag auf der 4. FEM/CAD-Tagung, Technische Universität
Darmstadt, 1996
1. Einführung
Die
Finite-Element-Methode stellt heute ein Standardverfahren für die
statische Berechnung von Bauteilen, insbesondere von Decken dar. Gegenüber
den herkömmlichen baustatischen Methoden handelt es sich bei der Finite-Element-Methode
um ein hochentwickeltes und leistungsfähiges Werkzeug, dessen Anwendung
aber auch besondere Statik-Kenntnisse erfordert. Wird die FEM - ohne die
notwendigen Kenntnisse - als ´black-box´-Methode angewandt,
sind Fehler häufig die Folge. Im Beitrag werden eine Reihe in der
Praxis aufgetretener und bei der statischen Prüfung durch den Prüfingenieur
aufgefundener Fälle von Fehlern bei der FEM-Anwendung behandelt. Die
untersuchten Fälle zeigen, daß gewisse Grundlagenkenntnisse
für einen sachgemäßen Umgang mit der Methode notwendig
sind. Es wird versucht, die Fehlerquellen zu systematisieren und Hinweise
zu geben, wie im Bürobetrieb Fehler vermieden werden können.
2. Modellbildung
Die
FEM eröffnet die Möglichkeit, äußerst komplizierte
Modelle statisch sehr detailliert zu untersuchen. Dadurch
ergeben sich Fehlerquellen bei der Modellbildung, die bei einer konventionellen
Berechnung mit einem vereinfachten statischen System nicht auftreten.
2.1 Unterzüge
Die
Modellbildung von Unterzügen, für die es mehrere Möglichkeiten
gibt, erfolgt bei vielen Programmen nach der Eingabe der Geometriewerte
automatisch. Wesentlich ist eine realitätsnahe Erfassung der Biegesteifigkeit
unter Berücksichtigung der Exzentrizität [1]. Der Einspanngrad
eines Unterzugs in einspannende Bauteile darf nicht zu hoch angesetzt werden.
Fallbeispiel
1: Ein
Unterzug mit einer Höhe von ca. 80 cm wurde seitlich zu 100% eingespannt
berechnet, obwohl der Unterzug an eine Platte mit nur 25 cm Dicke angeschlossen
war. Dadurch war die Feldbewehrung des Unterzugs erheblich unterbemessen
worden. Die Einspannbewehrung wurde vom Programm mit dem inneren Hebelarm
des Unterzugs bemessen, anstatt mit dem kleineren inneren Hebelarm der
Platte.
2.2 Modellbildung
bei Balkonplatten
Beim
Anschluß von Balkonplatten an Deckenplatten treten infolge der Drillmomente
im Eckbereich erhöhte Momente auf (Bild 1).
|
|
|
System
|
Durchbiegungen
|
Hauptmomente
|
|
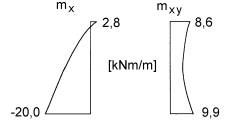 Schnitt
A-A
Schnitt
A-A
|
Bild
1: Allseitig
gelenkig gelagerte Platte mit auskragender Balkonplatte
|
In
der Praxis wird häufig der Schöck-Isokorb als tragendes Wärmedämmelement
beim Anschluß von Balkonplatten verwendet. Aufgrund seiner Konstruktion
kann der Isokorb ausschließlich Biegemomente in einer Richtung übertragen
(Bild 2). Das statische Modell darf daher keine Übertragung von Drillmomenten
zulassen. Dies erreicht man, indem man die Balkonplatte selbst nicht idealisiert
und die Lasten aus dem Balkon als Linienlast und als Krempelmoment auf
der Deckenplatte ansetzt. Ist zum Zeitpunkt der Berechnung noch nicht definitiv
geklärt, ob Schöck-Isokörbe eingebaut werden, können
sich der Fehler in der Modellbildung, bei nachträglichen Entscheidungen
hierüber, leicht in die statische Berechnung "einschleichen".
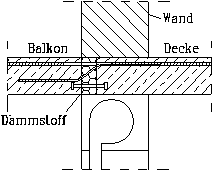
Isokorb |
Modellbildung |
Bild
2:
Schöck-Isokorb
2.3 Gebäudesteifigkeit
bei Bodenplatten
Die
Steifigkeit aufgehender Stahlbetonwände beeinflußt die Schnittgrößen
in Bodenplatten erheblich. In der Regel werden sie als Überzüge,
die durch Stabelemente modelliert werden, berücksichtigt.
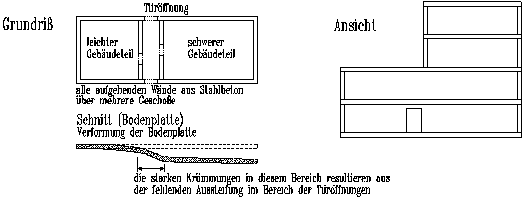
Fallbeispiel
2: Zwei
unterschiedlich schwere Gebäudeteile befinden sich auf einer gemeinsamen
Bodenplatte (Bild 3). Die aussteifende Wirkung der Seitenwände, die
durch Türöffnungen unterbrochen sind, wurde bei der FEM-Berechnung
der elastisch gebetteten Platte zwischen den beiden Gebäudeteilen
vernachlässigt. Die dadurch ermittelten hohen Beanspruchungen in der
Bodenplatte treten in Wirklichkeit nicht auf, da die Seitenwände des
steifen Kastens die Verschiebungen der Bodenplatte koppeln.
Bild
3: Bodenplatte
mit Gebäude
Fallbeispiel
3: Die
aufgehenden Wände bei einer als elastisch gebettete Platte berechneten
Bodenplatte wurden als starre Lager in ein FE-Programm eingegeben und die
Platte danach bewehrt. Es
ergaben sich völlig fehlerhafte Bemessungsschnittgrößen
in der Bodenplatte, die quasi als Deckenplatte berechnet worden war, wie
z.B. negative Momente unterhalb der Wände und positive Momente in
den Feldern. Die statische
Untersuchung der Platte mußte neu durchgeführt werden.
2.4 Zugbeanspruchungen
und abhebende Kräfte
Rechnerische
Zugbeanspruchungen der Auflager sind nur möglich, sofern diese durch
Auflasten (Wände) überdrückt werden oder entsprechend rückverankert
werden. Ist dies nicht der Fall, sind abhebende Auflagerkräfte im
Rahmen einer nichtlinearen Berechnung auszuschließen oder die Platte
ist drillweich zu berechnen.
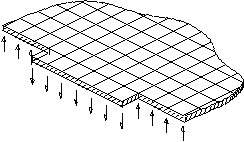
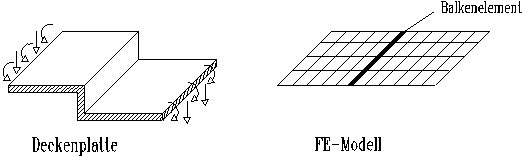
Fallbeispiel
4: Durch
die zu detaillierte Modellierung eines starr gelagerten Deckenvorsprungs
wurden hohe abhebende Kräfte erhalten, die nicht durch Auflasten überdrückt
wurden (Bild 4). Durch die
automatische Lastübergabe des Programms wurden die Auflagerkräfte
als vertikal nach oben wirkende Kräfte auf die darunterliegende Decke
aufge-bracht, obwohl eine Zuglastübertragung durch die Mauerwerkswände
nicht möglich ist. Durch
eine vereinfachte Modellierung im Bereich des Vor-sprungs oder u.U. auch
durch eine elastische Lagerung hätte der Fehler vermieden werden können.
Bild
4:
Detail einer Deckenplatte
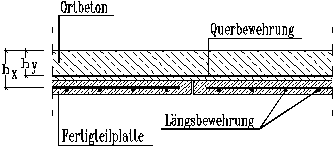
2.5 Elementdecken
Bei
der Bemessung von Fertigplatten mit statisch mitwirkender Ortbetonschicht
muß der kleinere innere Hebelarm in der Ortbetonschicht berücksichtigt
werden (Bild 4).
3. Ergebnisinterpretation
Um
die Ergebnisse sinnvoll interpretieren zu können, muß Klarheit
darüber bestehen, welche Tragwerksmodellierung zugrunde liegt und
welche Schnittgrößen im konkreten Fall von der FEM zuverlässig
ermittelt werden und bei welchen dies nicht der Fall ist [1]. Insbesondere
muß auch bei Flächentragwerken zwischen B- und D-Bereichen (Stabwerksmodelle),
die einer ergänzenden Untersuchung bedürfen, unterschieden werden
[2]. Die Berechnungsergebnisse
müssen in jedem Fall noch einmal kritisch geprüft und gegebenenfalls
ergänzt werden.
3.1 Unterzüge
Bei
der Bemessung von Unterzügen auf Biegung und Schub ist es besonders
wichtig, den Modellcharakter des berechneten statischen Systems vor Augen
zu haben [1].
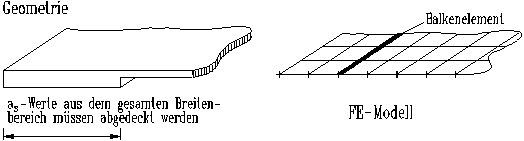
Fallbeispiel
5: Ein
breiter Unterzug einer Deckenplatte ist korrekt als exzentrischer Balken
modelliert worden (Bild 6). Im FE-Modell stellt der Unterzug ein Stabelement
(ohne Breite) dar, das zusätzlich zu den Plattenelementen eingefügt
wird. Das abzudeckende Gesamtmoment im wirklichen Unterzug setzt sich zusammen
aus dem rechnerischen Momentenanteil im Unterzug und dem Momentenanteil
in der Platte, bezogen auf den betrachteten Streifen. In der Bewehrungszeichnung
wurde allerdings aus-schließlich der Bewehrungsanteil des Balkens
eingebaut. Durch die erhebliche Breite des Unterzugs ergab sich in der
FE-Berechnung eine fast ebenso große Bewehrung in der Platte, die
allerdings noch im Verhältnis der inneren Hebelarme von Platte zu
Balken verringert werden kann. Ähnliches gilt für die Schubbewehrung
und den Schubspannungsnachweis im Unterzug.
Bild
6:
Breiter Unterzug einer Deckenplatte
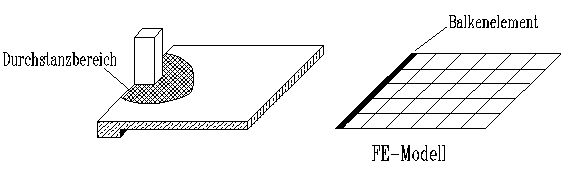
3.2 Durchstanzen
Der
Durchstanznachweis für Stützen bei Flachdecken oder Fundamentplatten
sollte mit der Stützenkraft, gegebenenfalls vermindert um die Querkräfte
anschließender Unterzüge, geführt werden. Die aus den Plattenquerkräften
ermittelten Schubspannungen sind hierfür in der Regel ungeeignet.
Fallbeispiel
6: Eine
hohe Einzellast wirkt am Rand einer Bodenplatte. Dieser Plattenbereich
ist verstärkt, d.h. die Platte hat am Rand einen Unterzug. Die
Einzellast wird in einen Querkraftanteil, der durch den Unterzug abgetragen
wird und einen Anteil, der in der Platte wirkt, aufgeteilt. Je nach der
Steifigkeit des Randunterzuges verbleibt in der Platte ein durchaus erheblicher
Querkraftanteil. Die sich aus diesem Anteil ergebende Durchstanzbewehrung
wurde beim statischen Nachweis vergessen (Bild
7).
Bild
7: Bodenplatte
mit Randverstärkung
3.3 Bemessungswerte
und Singularitäten von Schnittgrößen
Die
Bemessungspunkte sind an den relevanten Stellen zu wählen und es ist
zwischen Punkten mit singulären und Bereichen mit regulären Schnittgrößen
zu unterscheiden [1].
Fallbeispiel
7:
Ein Programm gab nur die (numerisch zuverlässigeren) Schnittgrößen
in Elementmitte aus. Da über den Wänden die Elementmitten
nicht auf der Wandkante lagen, erfolgte die Bemessung dort für ein
falsches, d.h. zu geringes Anschnittmoment.
3.4 Weitere
statische Nachweise, B- und D-Bereiche
Nach
der Durchführung einer FE-Berechnung ist zu prüfen, ob weitere,
im Rechengang nicht enthaltene statische Nachweise erforderlich sind. Auflager-
und Lasteinleitungsbereiche sind häufig Singularitätenstellen
und damit typische D-Bereiche, die eine konstruktive Durchbildung mit Stabwerkmodellen
erfordern [2]. Bewehrungswerte des FE-Programms dürfen keinesfalls
unreflektiert in die Bewehrungspläne übernommen werden.
Fallbeispiel
8: In
der Deckenplatte einer Tiefgarage wurde ein Versprung als Balken modelliert
(Bild 8). Diese Idealisierung gibt im Bereich des Versprungs den wirklichen
Kräfteverlauf nicht richtig wieder. Das Programm ermittelt ausschließlich
die für die Querkraftbemessung des Balkens erforderliche Bewehrung.
Der Einfluß des von unten angreifenden Querkraftanteils der Platte
und die Übertragung des Plattenbiegemoments wurden nicht berücksichtigt.
Bild
8: Deckenversprung
3.5
Verankerungslängen und Versatzmaß
FE-Programme
ermitteln keine exakten Zugkraftdeckungslinien und berücksichtigen
somit kein Versatzmaß und keine Verankerungslängen. Man darf
also die Bewehrung nicht dort enden lassen, wo im FE-Plott die erforderliche
Bewehrung endet.
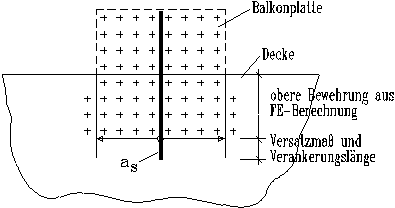
Fallbeispiel
9: Bei
einer Deckenplatte mit auskragender Balkonplatte muß die Stützbewehrung
mit ausreichender Länge in die obere Lage der Deckenplatte hineingeführt
werden (Bild 9).
Bild
9:
Decke mit Balkon
4.
Psychologische Aspekte
Psychologische
Effekte spielen bei der Computeranwendung, insbesondere bei FE-Programmen,
eine nicht zu unterschätzende Rolle. Je komplexer ein Programm ist,
desto mehr tendiert der Anwender dazu die Ergebnisse zu glauben, weil er
sie nicht mehr ohne weiteres überprüfen kann. Dies gilt verstärkt,
wenn Hintergrundkenntnisse über die FEM fehlen.
Statische
Berechnungen müssen häufig unter einem enormen Zeitdruck erstellt
werden. Dies verleitet dazu notwendige Kontrollen der Berechnung zu unterlassen.
Fallbeispiel
10: Eine
Bodenplatte wurde aufgrund eines Eingabefehlers mit einem Bettungsmodul
von 10000 MN/m3 anstelle von 10 MN/m3 bemessen (Fehlerfaktor
1000!). Der Aufsteller der Statik führte keine Plausibilitätskontrolle
durch, weshalb dieser Fehler von ihm nicht erkannt wurde.
Fallbeispiel
11: Ein
kastenförmiges Brückenwiderlager wurde mit einem FE-Faltwerkmodell
mit dem einseitigen Vekehrslastfall „Stellung eines SLW nahe der linken
Flügelwand“, der für die linke Flügelwand bemessungsbestimmend
war, berechnet. Der Konstrukteur übernahm die Angaben des FE-Ausgabeprotokolls
und bewehrte folglich die linke Flügelwand stärker als die rechte.
Er hatte nicht bedacht, daß die FE-Ausgabe nur für die linke
Symmetriehälfte gültig war und die rechte Flügelwand aus
Symmetriegründen (Stellung des SLW nahe der rechten Flügelwand)
identisch wie die linke Flügelwand hätte bewehrt werden sollen.
5.
Programmfehler
Programmfehler
treten meist in der Benutzeroberfläche oder bei der Generierung von
FE-Daten aus Gebäude-Geometriedaten auf. Sie
sind aber auch im Berechnungsteil des Programms nicht auszu-schließen.
Fallbeispiel
12: Im
Durchlaufträgerprogramm eines renommierten Softwarehauses kam es bei
der Änderung der Programmversion dazu, daß der Lastfall ´Einzelmoment
im Feld´ fehlerhaft berechnet wurde. Die alte Version dieses Programms
berechnete diesen Lastfall noch richtig.
Fallbeispiel
13: An
einem "schmalen" Deckendurchbruch neben einer Stütze wurde
eine Stützbewehrung im Öffnungsbereich berechnet, wobei der Durchbruch
als Öffnung eingegeben wurde. Es waren auch im Bereich der Öffnung
fälschlicherweise Finite Elemente generiert worden. Eine Vergrößerung
der Breite des Deckendurchbruchs führte zu richtigen Ergebnissen.
6.
Fehlerquellen im Büroalltag
Erfahrungsgemäß
haben Fehler vor allem folgende Ursachen:
· Zeitdruck
· fehlende
Plausibilitätskontrollen
· “Computergläubigkeit“
· nicht
ausreichende Beschäftigung mit komplexen FE-Programmen
· Nicht-Bauingenieure
(z.B. Mathematiker) führen FE-Berechnungen durch
· fehlende
Durchsicht der gezeichneten Pläne durch einen Ingenieur
· Kommunikationsprobleme
(z.B. Urlaubsvertretung)
´der eine verläßt sich auf den anderen´
· Programmierfehler
· Bei
automatischen Programmabläufen geht der Überblick verloren
Daß
auch Fehler mit schwerwiegenden Folgen gemacht werden können, zeigt
der Schadensfall an der Bohrplattform Sleipner A, bei der die fehlerhafte
Umsetzung einer Computerberechnung in einen Bewehrungsplan die Ursache
für den Untergang war [3].
7.
Qualitätssicherung von FE-Berechnungen
Die
zuverlässige Durchführung einer FE-Berechnungen erfordert eine
anschließende Qualitätssicherung. Die folgende Checkliste
kann hierbei hilfreich sein:
· Wurden
die Eingabewerte nochmals sorgfältig geprüft?
· Stimmen
die Verformungen und Schnittgrößenverläufe mit dem erwarteten
Tragverhalten überein (z.B. auch Symmetriebedingungen)?
· Wurden
die Unterzüge richtig modelliert und der Einspanngrad realitätsnah
angesetzt?
· Wurden
(nachträglich) Isokörbe eingebaut, die die Bewehrung beeinflussen?
· Wurde
die Gebäudesteifigkeit bei Bodenplatten sinnvoll modelliert?
· Ist
die FE-Diskretisierung an allen maßgebenden Stellen ausreichend fein?
· Sind
die Bemessungspunkte an allen maßgebenden Stellen sinnvoll gewählt?
· Treten
nicht übertragbare Zugspannungen oder abhebende Kräfte auf?
· Wurde
an Unterzügen die Überlagerung mit den Plattenschnittgrößen
bei der Biege- und Schubbemessung berücksichtigt?
· Wurden
alle erforderlichen Durchstanznachweise geführt, auch an Stützen
mit Unterzügen?
· Wurden
singuläre Stellen richtig und sinnvoll bemessen?
· Wurden
alle D-Bereiche konstruktiv richtig bewehrt? Maßgebende
Stellen sind:
* Lasteinleitungsbereiche (Aufhängebewehrung
u.a.)
* Auflager
· Sprünge
und Knicke im Querschnitt (Bewehrung zur Lastumleitung)
· Sind
Verankerungslängen und Versatzmaß berücksichtigt?
· Wurden
die erforderlichen Nachweise für den Gebrauchzustand (zulässige
Durchbiegung, Rissesicherheit) geführt?
Die
computerunterstützte Tragwerksplanung kann nur dann ein wirkliche
Hilfe für den Tragwerksplaner sein, wenn bei aller Informationsfülle
im Detail die wesentlichen Elemente des Tragverhaltens überschaubar
bleiben und damit die statische Untersuchung vom Tragwerksplaner auch verantwortet
werden kann.
Literatur
[1] Werkle,
Horst, Finite Elemente in der Baustatik, Teil 1: Lineare Statik der Stab-
und Flächentragwerke, Vieweg, Wiesbaden, 1995
[2] Schäfer,
Kurt, FE-Berechnung oder Stabwerksmodelle?, Finite Elemente in der Baupraxis,
Ernst & Sohn, Berlin, 1995
[3] Reineck,
Karl-Heinz, Der Schadensfall Sleipner und die Folgerungen für den
computerunterstützten Entwurf von Tragwerken aus Konstruktionsbeton,
Finite Elemente in der Baupraxis, Ernst & Sohn, Berlin, 1995
zurück